DSA Trees
Trees
Because each node in the Tree data structure can be linked to other nodes and includes data, it is comparable to Linked Lists.
Data structures like arrays, queues, stacks, and linked lists have all been discussed earlier. Since all of these structures are linear, every component in the sequence comes right after the other. But trees are not like other things. A Tree’s ability to support numerous ‘next’ components in a single element allows the data structure to branch off in different ways.
The reason the data structure is named a “tree” is that, as seen in the image below, it resembles a tree but is turned upside down.
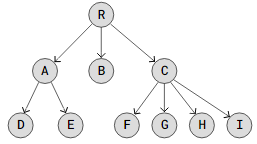
The Tree data structure has numerous applications.
- Hierarchical Data: file systems, organizational charts, etc.
- Databases: A means of retrieving data quickly.
- Routing Tables: Used for routing data in network algorithms.
- Sorting/Searching: Used for sorting data and searching for data.
- Priority Queues: Binary heaps and other trees are frequently used to construct priority queue data structures.
Tree Terminology and Rules
Explore the vocabulary related to the tree data structure by utilizing the interactive tree visualization provided below.
==== example mukavu ====
The root node is the initial node in a tree.
An edge is a connection that joins two nodes.
A parent node and its offspring nodes are connected. An internal node is another term for a parent node.
A node may have one, many, or none at all as offspring.
There can only be one parent node per node.
Leaf nodes are nodes that do not have connections to other child nodes.
The maximum number of edges that connect a root node to a leaf node is known as the tree height. The tree above is two stories tall.
The greatest number of edges that separate a node from a leaf node is its height.
The total number of nodes in the tree equals its size.
Types of Trees
In computer science, trees are a basic type of data structure that are used to depict hierarchical relationships. Many important tree species are covered in this session.
Binary trees: The left child node and the right child node are the two maximum children of each node. More intricate tree types like AVL and Binay Search Trees are built on top of this framework.
Binary Search Trees (BSTs): A kind of Binary Tree in which the value of each node is higher on the right child node and lower on the left child node.
AVL Trees: A particular kind of Binary Search Tree that self-balances to ensure that the height difference between the left and right subtrees for each node is kept to a minimum. Rotations are used to keep this equilibrium when nodes are added or removed.
The next sections provide a detailed description of each of these data structures, along with instructions for implementing animations.
