Insertion Sort
For a general definition of time complexity, see this page.
Insertion Sort Time Complexity
If the array is already sorted, but with the highest values at the top, that is the worst case scenario for Insertion Sort. This is due to the fact that each new value in this situation has to “move through” the entire sorted portion of the array.
The Insertion Sort algorithm performs the following operations on the initial elements:
- The 1st value is already in the correct position.
- The 2nd value must be compared and moved past the 1st value.
- The 3rd value must be compared and moved past two values.
- The 3rd value must be compared and moved past three values.
- And so on..
This pattern can be followed to determine the total number of operations for values of n:
===formula===
This is a well-known mathematical series that can be expressed as follows:
===formula==
We obtain the following time complexity for the Insertion Sort method using Big O notation:
===formula===
This is one way to represent the time complexity:
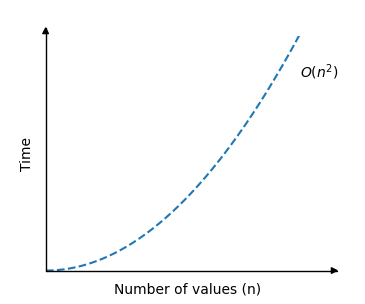
As you can see, when the number of values is raised, Insertion Sort takes a lot more time.
Insertion Sort Simulation
Use the simulation below to see how the theoretical time complexity O(n2)(red line) compares with the number of operations of actual Insertion Sorts.
===image===
There is a significant distinction between the best, average, and worst case possibilities for Insertion Sort. You can test it by executing the various simulations mentioned above.
The red line above represents the theoretical upper bound time complexity O(n2), and the actual function in this case is 1.07⋅n2.
Remember that a function f(n) is said to be O(g(n)) if we have a positive constant C so that C⋅g(n)>f(n).
In this case f(n)is the number of operations used by Insertion Sort, g(n)=n2 and C=1.07.
