Counting Sort
For a general definition of time complexity, see this page.
Counting Sort Time Complexity
In order to reconstruct the array in a sorted manner, counting sort first counts the occurrence of distinct values.
Generally speaking, the Counting Sort algorithm operates quickly when the range of potential values k is less than the quantity of values n..
We must first count the number of operations the method performs in order to indicate the time complexity in Big O notation:
- Finding the maximum value: Every value must be evaluated once to find out if it is the maximum value, so n operations are needed.
- Initializing the counting array: With the maximum value in the array, we need k+1elements in the counting array to include 0. Every element in the counting array must be initialized, so k+1operations are needed.
- Every value we want to sort is counted once, then removed, so 2 operations per count, 2⋅noperations in total.
- Building the sorted array: Create nelements in the sorted array: noperations.
In total we get:
===formula===
We can use Big O notation to generate a simpler statement that represents time complexity based on what we have heard before regarding time complexity:
===formula===
It has already been mentioned that Counting Sort is effective when the range of different values k is relatively small compared to the total number of values to be sorted n. We can now see this directly from the Big O expression O(n+k).
Just imagine for example that the range of different numbers k is 10 times as large as the number of the values to be sorted. In such a case we can see that the algorithm uses most of its time on handling the range of different numbers k, although the actual number of values to be sorted n is small in comparison.
Because the time complexity of Counting Sort is influenced by the range of values k, it is not as simple to display the time complexity in a graph or to create a simulation of the time complexity as we have done with the other algorithms.
The graphic that illustrates the range of time complexity for Counting Sort is presented below, along with an explanation of the best and worst case scenarios.
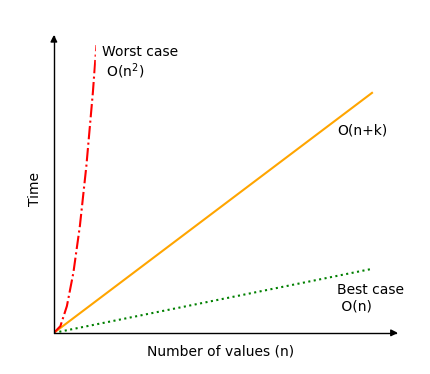
The best case scenario for Counting Sort would be to have the range kjust a fraction of n, let’s say k(n)=0.1⋅n. As an example of this, for 100 values, the range would be from 0 to 10, or for 1000 values the range would be from 0 to 100. In this case we get time complexity O(n+k)=O(n+0.1⋅n)=O(1.1⋅n) which is simplified to O(n).
The worst case however would be if the range is a lot larger than the input. Let’s say for an input of just 10 values the the range is between 0 and 100, or similarly, for an input of 1000 values, the range is between 0 and 1000000. In such a scenario, the growth of k is quadratic with respect to n, like this: k(n)=n2, and we get time complexity O(n+k)=O(n+n2) which is simplified to O(n2). A case that is even worse than this could also be constructed, but this case is chosen because it is relatively easy to understand, and perhaps not that unrealistic either.
As you can see, before selecting Counting Sort as your algorithm, it is crucial to take into account the range of values in relation to the number of items to be sorted. Additionally, remember that counting sort only functions with non-negative integer values, as stated at the start of the page.
Counting Sort Simulation
Run different simulations of Counting Sort to see how the number of operations falls between the worst case scenario O(n2)(red line) and best case scenario O(n)(green line).
===image===
As previously stated: if there are few numbers to sort (small k) and the numbers to be sorted have a wide range of values n Counting Sort method does not work well.
If we are holding n additionally k Thus, the number of operations is the same for the “Random,” “Descending,” and “Ascending” possibilities in the scenario above. This is due to the fact that all three scenarios have the same outcome: After setting up a counting array and counting the integers, a new sorted array is produced.
