DSA Shortest Path
The Shortest Path Problem
A well-known problem in computer science is the shortest path problem.
Finding the shortest path or route between two vertices (or nodes) in a graph is the definition of the shortest path issue.
A graph can represent anything in the shortest path problem, from a road network to a communication network, with roads, flight lines, or data cables serving as the edges and intersections, cities, or routers as the vertices.
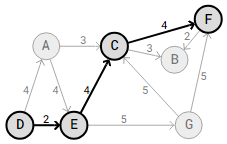
In the graph above, the shortest path with a total path weight of 2+4+4=10 is D->E->C->F from vertex D to vertex F. Although there are other alternative routes from D to F, they cannot be regarded as the shortest way because of their larger overall weight.
Solutions to The Shortest Path Problem
The shortest path between a single start vertex and every other vertex is found using Dijkstra’s algorithm and the Bellman-Ford algorithm.
The shortest path problem can be solved by examining all of the graph’s edges until we identify a path that allows us to move between two vertex points while utilizing the least amount of cumulative weight along each edge.
A path weight or path cost is the total of the weights along the edges that comprise the path.
Finding the shortest pathways between one start vertex and every other vertex is the goal of shortest path algorithms, such as Dijkstra’s algorithm and the Bellman-Ford algorithm.
Initially, the algorithms establish an infinitely long distance between the initial vertex and every other vertex. Additionally, when the algorithms execute, the edges connecting the vertices are repeatedly examined; as a result, shorter paths may be discovered repeatedly until the end, when the shortest paths are discovered.
An edge is said to be relaxed or relaxed whenever it is verified and results in a shorter path to a vertex being located and updated.
Positive and Negative Edge Weights
Certain algorithms, such as Dijkstra’s algorithm, are limited to finding the shortest paths in graphs with all of the edges being positive. Because we can conceptualize the connections connecting vertices as distances between locations, these graphs with positive distances are also the simplest to comprehend.
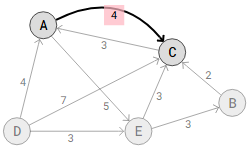
In the graph above, a positive edge weight of 4 from vertex A to vertex C indicates that we need to spend $4 to get from A to C, if we understand the edge weights as the amount of money lost by moving from one vertex to another.
However, graphs can also include negative edges, in which case the shortest pathways can be found using the Bellman-Ford algorithm.
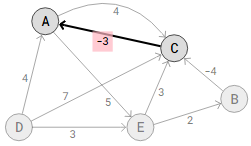
Similarly, the negative edge weight -3 from vertex C to vertex A in the preceding graph might be interpreted as an edge where there is more money to be made than money lost by going from C to A if the edge weights indicate money lost. Therefore, money lost is -3, meaning we are actually making $3 overall, if, for instance, the cost of gasoline is $5 for traveling from C to A and we get paid $8 for picking up products in C and delivering them in A.
Negative Cycles in Shortest Path Problems
It is difficult to find the shortest pathways on a graph with negative cycles.
A negative cycle is characterized by a path that is circular in shape and has a total path weight of negative for all of its edges.
The path A->E->B->C->A in the graph below is a negative cycle since the overall path weight is 5+2-4-4=-1.

An algorithm may always be performed again to find even shorter paths, which is why it is impossible to identify the shortest paths in a graph with negative cycles.
Assume, for illustration purposes, that we want to find the shortest path between vertex D and every other vertex in the graph above. By just walking the edge from D to E, we first determine that the distance is 3. However, after that, the distance to E becomes two if we walk one circuit in the negative cycle E->B->C->A->E. The distance decreases to one after walking one more round, and so on. The shortest distance can never be found since we can always walk one more circle in the negative cycle to find a lesser distance to E.
Fortunately, negative cycle identification can be applied to the Bellman-Ford algorithm, which operates on graphs with negative edges.
