DSA Dijkstra's
The Dutch computer scientist Edsger W. Dijkstra created Dijkstra’s shortest path method in 1956 while out shopping in Amsterdam with his fiancée and taking a twenty-minute coffee break.
The algorithm was created in order to evaluate a brand-new device known as ARMAC.
Dijkstra's Algorithm
The shortest path between each vertex and every other vertex is found using Dijkstra’s algorithm.
It accomplishes this by repeatedly determining the distance to each unvisited neighboring vertex by choosing the closest unvisited vertex and running that calculation.
==== EXAM MUKAVU ====
The shortest path problem can be solved most easily with Dijkstra’s algorithm, according to many.
For directed or undirected paths, single-source shortest path issues are solved using Dijkstra’s method. When an algorithm is single-source, it selects one vertex as the starting point and determines the shortest path between it and every other vertex.
When graphs include negative edges, Dijkstra’s algorithm is not applicable. Alternatively, the Bellman-Ford algorithm (explained on the following page) can be applied to graphs with negative edges.
Dijkstra’s algorithm requires three things in order to find the shortest path: it needs to know which vertex is the source, it needs a way to mark vertices as visited, and as it traverses the graph, it needs to keep track of the current shortest distance to each vertex, updating these distances whenever a shorter distance is discovered.
How it works:
1.Establish starting distances for each vertex, with the source vertex at 0 and the remaining vertices at infinity.
2.As the current vertex, select the unvisited vertex that is the furthest from the beginning. As a result, the source will always be the current vertex in the algorithm.
3.Determine the distance from the source for each unvisited neighbor vertex of the current vertex, then update the value if the newly calculated distance is less.
4.We designate the present vertex as visited since we are finished working with it. No further checks are made on a visited vertex.
5.To select a new current vertex, go back to step 2 and repeat these steps until all vertices have been visited.
6.The shortest path between each vertex in the graph and the source vertex is what remains at the end.
When a vertex in the animation above is designated as visited, both the vertex and its edges fade to show that Dijkstra’s algorithm has finished with that vertex and won’t be returning.
Note:The simplest path cost to each vertex is provided by this variant of Dijkstra’s algorithm, but the path itself is not disclosed. The shortest path cost value of 10, for instance, is obtained to vertex F in the animation above, but the method does not indicate which vertices (D->E->C->D->F) comprise this shortest path. This capability will be added later on this page.
A Detailed Dijkstra Simulation
To learn more about how Dijkstra’s algorithm finds the shortest distances from vertex D on a particular graph, run the simulation below.
==== EXAM MUKAVU ====
This simulation demonstrates how to compute the distances between any vertex and vertex D by constantly selecting the subsequent vertex as the next unexplored vertex from the beginning point.
Get complete information on how Dijkstra’s algorithm determines the shortest distances by following the detailed explanation provided below.
Manual Run Through
Consider the Graph below.
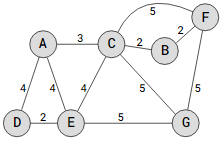
The goal is to determine the shortest path, with path weight 2+4=6, from the source vertex, D, to all other vertices. For instance, the shortest path to C is D->E->C.
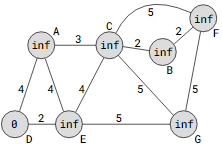
Dijkstra’s technique employs an array containing the distances to all other vertices and sets these distances to infinite, or a very large amount, at first in order to discover the shortest path. Additionally, 0 represents the distance to the source, or the vertex from whence we originate.
distances = [inf, inf, inf, 0, inf, inf, inf]
#vertices [ A , B , C , D, E , F , G ]
The starting vertex D and the initial limitless distances to other vertices are depicted in the graphic below. Since vertex D is the beginning point, its distance value is 0.
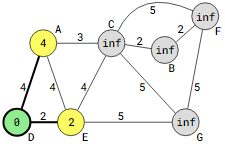
After setting vertex D as the current vertex, Dijkstra’s algorithm measures the separation between the two adjacent vertices. The new distance between vertices A and E is updated with the edge weights because the initial distance to these is limitless. As a result, the distances at vertex A and vertex E are adjusted from inf to 4 and 2, respectively. This method of adjusting the distance values is known as “relaxing,” as was discussed on the preceding page.
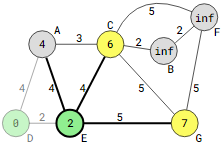
Vertex D is regarded as visited after vertices A and E have relaxed; it will not be visited again.
Among the previously unvisited vertices, the vertex with the lowest distance to the source vertex (vertex D) must be the next vertex to be selected as the current vertex. As a result, after vertex D, vertex E is selected as the current vertex.
It is now necessary to determine, and if necessary, update, the distance from vertex E to all neighboring and unvisited vertices.
The estimated distance is 2+4=6 from vertex D to vertex A via vertex E. However, the distance to vertex A has already decreased to 4, meaning that it has not been changed.
The distance to vertex C is updated since the estimated distance is 2+4=6, which is less than infinity.
In a similar manner, 2+5=7 is the adjusted distance to node G.
Since vertex A is the closest to D of all the unvisited vertices, it will be visited first.
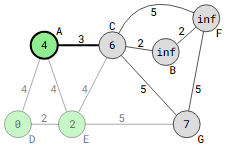
The distance to vertex C is not updated since the estimated distance, via vertex A, is 4+3=7, which is greater than the value that is currently set.
Vertex C is currently the next visited vertex, having the smallest distance from vertex D of the remaining unvisited vertices. Vertex A has now been marked as visited.
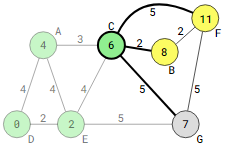
Updated distances of 6+5=11 for vertex F and 6+2=8 for vertex B are obtained.
Distance to vertex G is not updated since the distance calculated from vertex C to vertex G is 6+5=11, which is greater than the predetermined value of 7.
Since vertex G has the smallest distance between the remaining unvisited vertices, it will be visited first, and vertex C is marked as visited.
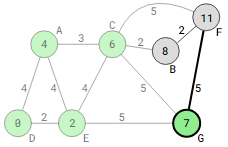
Vertex F is currently 11 distance away. The distance to vertex F is not updated because this is less than the distance from G, which is 7+5=12.
Because vertex B is the closest to the remaining unvisited vertices, it is designated as the current vertex and vertex G is recorded as visited.
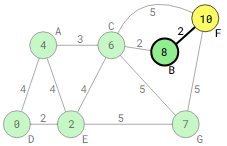
Due to the fact that it is less than the current distance of 11, the new distance to F via B is 8+2=10.
Dijkstra’s procedure is complete since vertex B has been marked as visited and there is nothing to check for the final unvisited vertex F.
The lowest distance between the source vertex D and every other vertex in the graph is the outcome of each vertex only having been visited once.
Implementation of Dijkstra's Algorithm
Dijkstra’s algorithm is implemented by creating a Graph class. The graph’s edges and vertices are represented by the graph:
class Graph:
def __init__(self, size):
self.adj_matrix = [[0] * size for _ in range(size)]
self.size = size
self.vertex_data = [''] * size
def add_edge(self, u, v, weight):
if 0 <= u < self.size and 0 <= v < self.size:
self.adj_matrix[u][v] = weight
self.adj_matrix[v][u] = weight # For undirected graph
def add_vertex_data(self, vertex, data):
if 0 <= vertex < self.size:
self.vertex_data[vertex] = data
Line 3: To store all of the edges and edge weights, we build the adj_matrix. The starting point is set to 0.
Line 4: The graph’s size is determined by its vertex count.
Line 5: All of the vertices’ names are stored in the vertex_data.
Lines 7–10: To create an edge with weight weight from vertex u to vertex v, using the add_edge function.
Lines 12–14: To add a vertex to the graph, use the add_vertex_data method. The vertex argument contains the index where the vertex should be, and data is the vertex’s name.
The Dijkstra algorithm’s running function is also included in the Graph class:
def dijkstra(self, start_vertex_data):
start_vertex = self.vertex_data.index(start_vertex_data)
distances = [float('inf')] * self.size
distances[start_vertex] = 0
visited = [False] * self.size
for _ in range(self.size):
min_distance = float('inf')
u = None
for i in range(self.size):
if not visited[i] and distances[i] < min_distance:
min_distance = distances[i]
u = i
if u is None:
break
visited[u] = True
for v in range(self.size):
if self.adj_matrix[u][v] != 0 and not visited[v]:
alt = distances[u] + self.adj_matrix[u][v]
if alt < distances[v]:
distances[v] = alt
return distances
Lines 18–19: All vertices in the distances array have their initial distance set to infinity, with the exception of the start vertex, which has a distance of 0.
Line 20: To indicate that they have not been visited in the visited array, all vertices are first set to False.
Line 23-28: There is a current vertex next to it. We’ll examine this vertex’s outgoing edges to see if any shorter lengths can be discovered. It is the least distanced unvisited vertex from the beginning.
Lines 30-31: The method terminates if the next current vertex cannot be located. In other words, every vertex that can be reached from the source has been visited.
Line 33: After relaxing neighboring vertices, the present vertex is marked as visited. Because we don’t have to measure the distance to the current vertex, this is more efficient.
Lines 35–39: If the newly computed distance is less than the previous one, the distances are updated for the unvisited neighboring vertices.
The vertices and edges need to be defined in order to initialize the particular graph after the Graph class has been defined. The whole code for this Dijkstra’s algorithm example is as follows:
Example
Python:
class Graph:
def __init__(self, size):
self.adj_matrix = [[0] * size for _ in range(size)]
self.size = size
self.vertex_data = [''] * size
def add_edge(self, u, v, weight):
if 0 <= u < self.size and 0 <= v < self.size:
self.adj_matrix[u][v] = weight
self.adj_matrix[v][u] = weight # For undirected graph
def add_vertex_data(self, vertex, data):
if 0 <= vertex < self.size:
self.vertex_data[vertex] = data
def dijkstra(self, start_vertex_data):
start_vertex = self.vertex_data.index(start_vertex_data)
distances = [float('inf')] * self.size
distances[start_vertex] = 0
visited = [False] * self.size
for _ in range(self.size):
min_distance = float('inf')
u = None
for i in range(self.size):
if not visited[i] and distances[i] < min_distance:
min_distance = distances[i]
u = i
if u is None:
break
visited[u] = True
for v in range(self.size):
if self.adj_matrix[u][v] != 0 and not visited[v]:
alt = distances[u] + self.adj_matrix[u][v]
if alt < distances[v]:
distances[v] = alt
return distances
g = Graph(7)
g.add_vertex_data(0, 'A')
g.add_vertex_data(1, 'B')
g.add_vertex_data(2, 'C')
g.add_vertex_data(3, 'D')
g.add_vertex_data(4, 'E')
g.add_vertex_data(5, 'F')
g.add_vertex_data(6, 'G')
g.add_edge(3, 0, 4) # D - A, weight 5
g.add_edge(3, 4, 2) # D - E, weight 2
g.add_edge(0, 2, 3) # A - C, weight 3
g.add_edge(0, 4, 4) # A - E, weight 4
g.add_edge(4, 2, 4) # E - C, weight 4
g.add_edge(4, 6, 5) # E - G, weight 5
g.add_edge(2, 5, 5) # C - F, weight 5
g.add_edge(2, 1, 2) # C - B, weight 2
g.add_edge(1, 5, 2) # B - F, weight 2
g.add_edge(6, 5, 5) # G - F, weight 5
# Dijkstra's algorithm from D to all vertices
print("\nDijkstra's Algorithm starting from vertex D:")
distances = g.dijkstra('D')
for i, d in enumerate(distances):
print(f"Distance from D to {g.vertex_data[i]}: {d}")
Dijkstra's Algorithm on Directed Graphs
Very few modifications are required to run Dijkstra’s method on directed graphs.
To make the adjacency matrix non-symmetric, we merely need to remove one line of code, much like the change we needed for cycle detection for directed graphs.
Now that this directed graph is in place, let’s execute Dijkstra’s algorithm starting at vertex D.
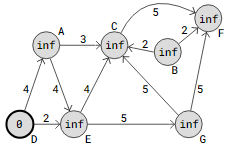
The directed graph’s Dijkstra’s algorithm is applied here, with D serving as the source vertex:
Example
Python:
class Graph:
def __init__(self, size):
self.adj_matrix = [[0] * size for _ in range(size)]
self.size = size
self.vertex_data = [''] * size
def add_edge(self, u, v, weight):
if 0 <= u < self.size and 0 <= v < self.size:
self.adj_matrix[u][v] = weight
#self.adj_matrix[v][u] = weight For undirected graph
def add_vertex_data(self, vertex, data):
if 0 <= vertex < self.size:
self.vertex_data[vertex] = data
def dijkstra(self, start_vertex_data):
start_vertex = self.vertex_data.index(start_vertex_data)
distances = [float('inf')] * self.size
distances[start_vertex] = 0
visited = [False] * self.size
for _ in range(self.size):
min_distance = float('inf')
u = None
for i in range(self.size):
if not visited[i] and distances[i] < min_distance:
min_distance = distances[i]
u = i
if u is None:
break
visited[u] = True
for v in range(self.size):
if self.adj_matrix[u][v] != 0 and not visited[v]:
alt = distances[u] + self.adj_matrix[u][v]
if alt < distances[v]:
distances[v] = alt
return distances
g = Graph(7)
g.add_vertex_data(0, 'A')
g.add_vertex_data(1, 'B')
g.add_vertex_data(2, 'C')
g.add_vertex_data(3, 'D')
g.add_vertex_data(4, 'E')
g.add_vertex_data(5, 'F')
g.add_vertex_data(6, 'G')
g.add_edge(3, 0, 4) # D -> A, weight 5
g.add_edge(3, 4, 2) # D -> E, weight 2
g.add_edge(0, 2, 3) # A -> C, weight 3
g.add_edge(0, 4, 4) # A -> E, weight 4
g.add_edge(4, 2, 4) # E -> C, weight 4
g.add_edge(4, 6, 5) # E -> G, weight 5
g.add_edge(2, 5, 5) # C -> F, weight 5
g.add_edge(1, 2, 2) # B -> C, weight 2
g.add_edge(1, 5, 2) # B -> F, weight 2
g.add_edge(6, 5, 5) # G -> F, weight 5
# Dijkstra's algorithm from D to all vertices
print("Dijkstra's Algorithm starting from vertex D:\n")
distances = g.dijkstra('D')
for i, d in enumerate(distances):
print(f"Shortest distance from D to {g.vertex_data[i]}: {d}")
The shortest paths from vertex D, as determined by Dijkstra’s algorithm, are displayed in the picture below.
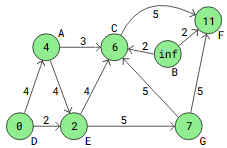
This outcome, which applies Dijkstra’s method to the undirected graph, is comparable to the preceding example. There’s a crucial distinction, though: in this instance, vertex B cannot be reached from D. As a result, the path can no longer pass through vertex B, making the shortest distance from D to F 11 instead of 10.
Returning The Paths from Dijkstra's Algorithm
Dijkstra’s algorithm may yield not only the shortest path values but also, with minor modifications, the actual shortest paths. For instance, the procedure can return that the shortest path is “D->E->C->B->F” rather than just “10” when calculating the shortest path from vertex D to vertex F.
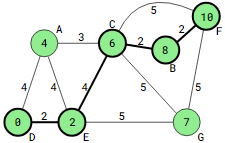
We build a predecessors array to store the preceding vertex in the shortest path for every vertex in order to return the path. The shortest path for each vertex can be found by going back and using the predecessors array.
Example
Python:
class Graph:
# ... (rest of the Graph class)
def dijkstra(self, start_vertex_data):
start_vertex = self.vertex_data.index(start_vertex_data)
distances = [float('inf')] * self.size
predecessors = [None] * self.size
distances[start_vertex] = 0
visited = [False] * self.size
for _ in range(self.size):
min_distance = float('inf')
u = None
for i in range(self.size):
if not visited[i] and distances[i] < min_distance:
min_distance = distances[i]
u = i
if u is None:
break
visited[u] = True
for v in range(self.size):
if self.adj_matrix[u][v] != 0 and not visited[v]:
alt = distances[u] + self.adj_matrix[u][v]
if alt < distances[v]:
distances[v] = alt
predecessors[v] = u
return distances, predecessors
def get_path(self, predecessors, start_vertex, end_vertex):
path = []
current = self.vertex_data.index(end_vertex)
while current is not None:
path.insert(0, self.vertex_data[current])
current = predecessors[current]
if current == self.vertex_data.index(start_vertex):
path.insert(0, start_vertex)
break
return '->'.join(path) # Join the vertices with '->'
g = Graph(7)
# ... (rest of the graph setup)
# Dijkstra's algorithm from D to all vertices
print("Dijkstra's Algorithm starting from vertex D:\n")
distances, predecessors = g.dijkstra('D')
for i, d in enumerate(distances):
path = g.get_path(predecessors, 'D', g.vertex_data[i])
print(f"{path}, Distance: {d}")
Lines 7 and 29: When the shortest path values are updated, the predecessors array is first started with None values and then updated with the right predecessor for each vertex.
Lines 33–42: The get_path function returns a string containing the shortest path from the start to the end vertex by using the predecessors array.
Dijkstra's Algorithm with a Single Destination Vertex
Suppose that all we want to do is figure out the shortest path between two vertices. For example, in the graph below, we want to discover the shortest distance between vertices D and F.
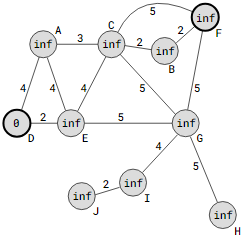
Dijkstra’s algorithm can be adjusted to only find the shortest path from the source to a single destination vertex by simply stopping the algorithm when the destination is reached, or visited. The Dijkstra’s algorithm is typically used to find the shortest path from one source vertex to all other vertices in the graph.
Because vertices H, I, and J are farther from D than vertice F is, Dijkstra’s algorithm will stop visiting F (the destination vertex) on the particular graph shown in the above image before moving on to vertices H, I, and J.
The estimated distances are displayed below once Dijkstra’s algorithm has determined the shortest path between D and F and has finished.
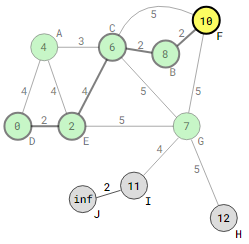
Vertex F in the preceding image has just updated to be 10 distances away from vertex B. The procedure terminates at F since it is the destination and the unvisited vertex with the lowest distance from D. Normally, F would be the next current vertex. J would be the subsequent vertices to get an updated distance of 11+2=13 from vertex I if the method continued.
The Dijkstra algorithm is used in the code below to determine the shortest path to a single destination vertex:
Example
Python:
class Graph:
# ... (existing methods)
def dijkstra(self, start_vertex_data, end_vertex_data):
start_vertex = self.vertex_data.index(start_vertex_data)
end_vertex = self.vertex_data.index(end_vertex_data)
distances = [float('inf')] * self.size
predecessors = [None] * self.size
distances[start_vertex] = 0
visited = [False] * self.size
for _ in range(self.size):
min_distance = float('inf')
u = None
for i in range(self.size):
if not visited[i] and distances[i] < min_distance:
min_distance = distances[i]
u = i
if u is None or u == end_vertex:
print(f"Breaking out of loop. Current vertex: {self.vertex_data[u]}")
print(f"Distances: {distances}")
break
visited[u] = True
print(f"Visited vertex: {self.vertex_data[u]}")
for v in range(self.size):
if self.adj_matrix[u][v] != 0 and not visited[v]:
alt = distances[u] + self.adj_matrix[u][v]
if alt < distances[v]:
distances[v] = alt
predecessors[v] = u
return distances[end_vertex], self.get_path(predecessors, start_vertex_data, end_vertex_data)
# Example usage
g = Graph(7)
# ... (rest of the graph setup)
distance, path = g.dijkstra('D', 'F')
print(f"Path: {path}, Distance: {distance}")
Line 20-23: If we are about to choose the destination vertex as the current vertex and mark it as visited, it means we have already calculated the shortest distance to the destination vertex, and Dijkstra’s algorithm can be stopped in this single destination case.
Time Complexity for Dijkstra's Algorithm
Given V as the number of vertices in our graph, Dijkstra’s algorithm’s time complexity is
O(V2)
This time complexity results from the need to search for the vertex with the smallest distance in order to select the next current vertex, which requires O(V) moment. We also need to account for the fact that this needs to be completed for each vertex that is connected to the source, which results in temporal complexity. O(V2.) regarding Dijkstra’s formula.
Instead (which are not covered in this tutorial), use a Min-heap or Fibonacci-heap data structure for the distances reduces the amount of time required to find the shortest distance vertex from O(V) to O(logV) This causes Dijkstra’s algorithm’s time complexity to improve.
O(V⋅logV+E)
where V is the graph’s vertex count, and E is the quantity of edges.
When utilizing a Min-heap data structure for Dijkstra’s method, the improvement is particularly strong for big and sparse graphs—that is, graphs with a high vertex count but a low edge count.
For dense graphs, where each vertex has an edge to nearly every other vertex, the Fibonacci-heap data structure provides a better way to implement Dijkstra’s method.
