DSA Ford-Fulkerson
The maximum flow problem is resolved by the Ford-Fulkerson algorithm.
Numerous applications can benefit from determining the maximum flow, including manufacturing, supply chain and logistics, network traffic optimization, and aircraft scheduling.
The Ford-Fulkerson Algorithm
The maximum flow problem for a directed graph is resolved by the Ford-Fulkerson algorithm.
The flow comes from a source vertex (s) and ends up in a sink vertex (t), and each edge in the graph allows a flow, limited by a capacity.
==== EXAMPLE MUKAVU ====
The Ford-Fulkerson method finds an augmented way—a path that has capacity—between the source and the sink, then sends as much flow as feasible through it.
Until the maximum flow is reached, the Ford-Fulkerson algorithm keeps looking for new routes to let additional flow through.
The maximum flow problem in the simulation above is resolved by the Ford-Fulkerson algorithm: It determines the maximum flow that the source vertex can send. s to the vertex of the sink t, and eight is the maximum flow.
The numbers in the simulation above are written in fractions, where the first number is the flow, and the second number is the capacity (maximum possible flow in that edge). So for example, 0/7 on edge s→v2, means there is 0 flow, with a capacity of 7 on that edge.
Note: Since the Ford-Fulkerson algorithm does not indicate how to identify a path where flow can be enhanced, it is frequently referred to as a method rather than an algorithm. This implies that it can be applied in many ways, leading to various temporal complexities. However, in this lesson, we’ll refer to it as an algorithm and find the paths using Depth-First-Search.
The Ford-Fulkerson algorithm’s fundamental step-by-step operation is shown here, but in order to truly comprehend it, we’ll need to delve into further depth later.
How it works:
1.Begin with no flow at any edge.
2.Locate an enhanced path where additional flow can be directed.
3.Determine the amount of flow that can be sent along that increased path by doing a bottleneck calculation.
4.In the enhanced path, increase the flow determined by the bottleneck calculation for every edge.
5.Until the maximum flow is reached, repeat steps 2-4. When a fresh augmented path is no longer possible to find, this occurs.
Residual Network in Ford-Fulkerson
In reality, the Ford-Fulkerson algorithm employs a residual network—a reconstruction of the original graph—to generate and utilize data.
Each edge in the residual network has a residual capacity, which is equal to the edge’s initial capacity less the edge’s flow. The remaining capacity in an edge with some flow is known as the residual capacity.
For example, if there is a flow of 2 in the v3→v4 edge, and the capacity is 3, the residual flow is 1 in that edge, because there is room for sending 1 more unit of flow through that edge.
Reversed Edges in Ford-Fulkerson
In order to return flow, the Ford-Fulkerson algorithm additionally employs a technique known as reversed edges. This helps to improve the overall flow.
For example, the last augmented path s→v2→v4→v3→t in the animation above and in the manual run through below shows how the total flow is increased by one more unit, by actually sending flow back on edge v4→v3, sending the flow in the reverse direction.
Sending flow back in the reverse direction on edge v3→v4 in our example meas that this 1 unit of flow going out of vertex v3, now leaves v3 on edge v3→t instead of v3→v4.
For every original edge in the network, a reverse edge is constructed in order to send flow back in the opposite direction of the edge. These reverse edges can then be used by the Ford-Fulkerson algorithm to send flow in the opposite direction.
A reversed edge has no flow or capacity, just residual capacity. The residual capacity for a reversed edge is always the same as the flow in the corresponding original edge. In our example, the edge v3→v4 has a flow of 2, which means there is a residual capacity of 2 on the corresponding reversed edge v4→v3.
This just means that when there is a flow of 2 on the original edge v3→v4, there is a possibility of sending that same amount of flow back on that edge, but in the reversed direction. Using a reversed edge to push back flow can also be seen as undoing a part of the flow that is already created.
The Ford-Fulkerson algorithm relies heavily on the concepts of reversed edges and a residual network with residual capacity on edges; we will discuss these concepts in greater detail as we apply the algorithm later in this section.
Manual Run Through
The graph does not initially have any flow.
The Ford-Fulkerson algorithm must increase flow in order to find the maximum flow, but it must first identify an enhanced path, which is the location where the flow can be raised.
Although the Ford-Fulkerson algorithm is sometimes referred to as a method rather than an algorithm, it actually does not indicate how such an augmented path is found; in this lesson, we will utilize Depth First Search (DFS) to locate the augmented paths for the Ford-Fulkerson methodology.
The first augmented path Ford-Fulkerson finds using DFS is s→v1→v3→v4→t.
The largest flow that may be sent through the augmented path, according to Ford-Fulkerson’s bottleneck calculation, is three. As a result, the flow is enhanced by three for each edge in this path.
The following steps must be repeated in the Ford-Fulkerson algorithm iteration after that:
2.Locate a fresh enhanced route.
3.Determine how much more flow there can be.
4.Increasing the flow in that direction in accordance with the edges
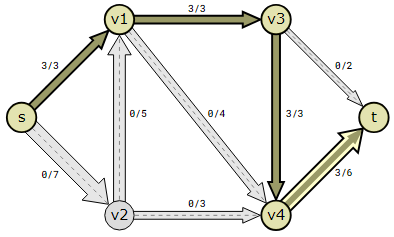
The next augmented path is found to be s→v2→v1→v4→v3→t, which includes the reversed edge v4→v3, where flow is sent back.
The path finding portion of the algorithm can find an augmented path where reversed edges can also be incorporated thanks to the Ford-Fulkerson concept of reversed edges.
In this specific case that means that a flow of 2 can be sent back on edge v3→v4, going into v3→t instead.
The flow can only be increased by 2 in this path because that is the capacity in the v3→t edge.
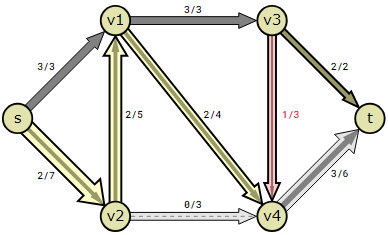
The next augmented path is found to be s→v2→v1→v4→t.
The flow can be increased by 2 in this path. The bottleneck (limiting edge) is v1→v4because there is only room for sending two more units of flow in that edge.
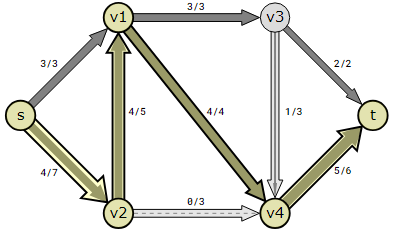
The next and last augmented path is s→v2→v4→t.
The flow can only be increased by 1 in this path because of edge v4→t being the bottleneck in this path with only space for one more unit of flow (capacity−flow=1).

There isn’t currently a way to identify a new augmenting path, meaning that more flow cannot be transmitted via from s to t), indicating that the Ford-Fulkerson procedure is complete when the maximum flow has been identified.
There is an eight-flow maximum. The figure above illustrates how the flow (8) exits the source is the same. vertex s as the stream entering the sink vertex t..
Furthermore, if you select any vertex other than s or t as you can see, there is an equal quantity of flow entering and exiting each vertex. This is known as conservation of flow, and it is a necessary condition for all directed graphs with flow and capacity at each edge.
Implementation of The Ford-Fulkerson Algorithm
The Ford-Fulkerson algorithm is implemented by creating a Graph class. The graph’s edges and vertices are represented by the graph:
class Graph:
def __init__(self, size):
self.adj_matrix = [[0] * size for _ in range(size)]
self.size = size
self.vertex_data = [''] * size
def add_edge(self, u, v, c):
self.adj_matrix[u][v] = c
def add_vertex_data(self, vertex, data):
if 0 <= vertex < self.size:
self.vertex_data[vertex] = data
Line 3: To store all of the edges and edge capacities, we build the adj_matrix. The starting point is set to 0.
Line 4: The graph’s size is determined by its vertex count.
Line 5: All of the vertices’ names are stored in the vertex_data.
Line 7-8: To add an edge with capacity c from vertex u to vertex v, use the add_edge method.
Lines 10–12: To add a vertex name to the graph, use the add_vertex_data method. The vertex name is data, and the vertex index is provided by the vertex parameter.
The dfs function for finding enhanced pathways using Depth-First-Search is also included in the Graph class:
def dfs(self, s, t, visited=None, path=None):
if visited is None:
visited = [False] * self.size
if path is None:
path = []
visited[s] = True
path.append(s)
if s == t:
return path
for ind, val in enumerate(self.adj_matrix[s]):
if not visited[ind] and val > 0:
result_path = self.dfs(ind, t, visited, path.copy())
if result_path:
return result_path
return None
Lines 15–18: When looking for an augmented path, the visited array helps to prevent returning to the same vertices. The path array contains the vertices that are part of the augmented path.
Line 20–21: After designating the current vertex as visited, it is appended to the path.
Lines 23–24: We have discovered an augmented path from the source vertex to the sink vertex, allowing that path to be returned if the current vertex is the sink node.
Lines 26–30: Beginning at the current vertex s, looping through every edge in the adjacency matrix, whereby ind stands for a neighboring node and val for the residual capacity on the edge leading to that vertex. Proceed to that node and carry on looking for a path from that vertex if the neighboring vertex is not visited and has remaining capacity on the edge to it.
Line 32: If no path is found, None is returned.
The final method we add to the Graph class is the fordFulkerson function:
def fordFulkerson(self, source, sink):
max_flow = 0
path = self.dfs(source, sink)
while path:
path_flow = float("Inf")
for i in range(len(path) - 1):
u, v = path[i], path[i + 1]
path_flow = min(path_flow, self.adj_matrix[u][v])
for i in range(len(path) - 1):
u, v = path[i], path[i + 1]
self.adj_matrix[u][v] -= path_flow
self.adj_matrix[v][u] += path_flow
max_flow += path_flow
path_names = [self.vertex_data[node] for node in path]
print("Path:", " -> ".join(path_names), ", Flow:", path_flow)
path = self.dfs(source, sink)
return max_flow
When there is an augmented path to increase flow in, the while loop increases the max_flow, which starts at 0.
Line 37: The enhanced route has been located.
Lines 39–42: The amount of flow that can be supplied through each edge in the enhanced path is determined.
Lines 44–46: An increase in flow causes a reduction in each forward edge’s residual capacity (capacity minus flow).
Line 47: This is an illustration of the reversed edge that the Ford-Fulkerson algorithm uses to send flow back (undone) on the initial forward edges. It’s critical to realize that Ford-Fulkerson created these flipped edges as imaginary edges in order to make the algorithm function; they weren’t in the original graph.
Line 49: max_flow increases by the same amount each time flow is raised over an augmented path.
Lines 51–52: Before the algorithm begins the subsequent iteration, this is simply for outputting the modified path.
The vertices and edges of the particular graph must be defined after the Graph class has been defined in order to initialize it. The full code for the Ford-Fulkerson algorithm example looks like this:
Example
Python:
class Graph:
def __init__(self, size):
self.adj_matrix = [[0] * size for _ in range(size)]
self.size = size
self.vertex_data = [''] * size
def add_edge(self, u, v, c):
self.adj_matrix[u][v] = c
def add_vertex_data(self, vertex, data):
if 0 <= vertex < self.size:
self.vertex_data[vertex] = data
def dfs(self, s, t, visited=None, path=None):
if visited is None:
visited = [False] * self.size
if path is None:
path = []
visited[s] = True
path.append(s)
if s == t:
return path
for ind, val in enumerate(self.adj_matrix[s]):
if not visited[ind] and val > 0:
result_path = self.dfs(ind, t, visited, path.copy())
if result_path:
return result_path
return None
def fordFulkerson(self, source, sink):
max_flow = 0
path = self.dfs(source, sink)
while path:
path_flow = float("Inf")
for i in range(len(path) - 1):
u, v = path[i], path[i + 1]
path_flow = min(path_flow, self.adj_matrix[u][v])
for i in range(len(path) - 1):
u, v = path[i], path[i + 1]
self.adj_matrix[u][v] -= path_flow
self.adj_matrix[v][u] += path_flow
max_flow += path_flow
path_names = [self.vertex_data[node] for node in path]
print("Path:", " -> ".join(path_names), ", Flow:", path_flow)
path = self.dfs(source, sink)
return max_flow
g = Graph(6)
vertex_names = ['s', 'v1', 'v2', 'v3', 'v4', 't']
for i, name in enumerate(vertex_names):
g.add_vertex_data(i, name)
g.add_edge(0, 1, 3) # s -> v1, cap: 3
g.add_edge(0, 2, 7) # s -> v2, cap: 7
g.add_edge(1, 3, 3) # v1 -> v3, cap: 3
g.add_edge(1, 4, 4) # v1 -> v4, cap: 4
g.add_edge(2, 1, 5) # v2 -> v1, cap: 5
g.add_edge(2, 4, 3) # v2 -> v4, cap: 3
g.add_edge(3, 4, 3) # v3 -> v4, cap: 3
g.add_edge(3, 5, 2) # v3 -> t, cap: 2
g.add_edge(4, 5, 6) # v4 -> t, cap: 6
source = 0; sink = 5
print("The maximum possible flow is %d " % g.fordFulkerson(source, sink))
Time Complexity for The Ford-Fulkerson Algorithm
The Ford-Fulkerson algorithm’s temporal complexity is dependent on the number of vertices (V), edges, and E, and it truly changes depending on the maximum flow f on the graph as well.
The explanation for the variation in temporal complexity with maximum flow f in the graph is due to the fact that a graph with a high throughput will have more augmented paths, which will increase flow. Consequently, the DFS technique responsible for locating these augmented paths will need to execute more times.
Depth-first search (DFS) has time complexity O(V+E).
For every new augmented path, DFS executes once. In the event where every augmented graph increases flow by one unit, DFS would need to execute f times, or as many times as the maximum flow is calculated.
This indicates that the Ford-Fulkerson algorithm’s time complexity while employing DFS is
O((V+E)⋅f)
For dense graphs, where E>V, time complexity for DFS can be simplified to O(E), which means that the time complexity for the Ford-Fulkerson algorithm also can be simplified to
O(E⋅f)
Although it is difficult to define precisely, a dense graph is one that has a large number of edges.
The Edmonds-Karp method is the next technique we shall discuss that determines maximum flow.
Although the Edmonds-Karp algorithm employs BFS rather than DFS to locate augmented pathways, it requires less iterations to find maximum flow than the Ford-Fulkerson approach.
