DSA Edmonds-Karp
The maximum flow problem is resolved by the Edmonds-Karp method.
Numerous applications can benefit from determining the maximum flow, including manufacturing, supply chain and logistics, network traffic optimization, and aircraft scheduling.
The Edmonds-Karp Algorithm
For a directed graph, the maximum flow problem can be solved using the Edmonds-Karp algorithm.
The source vertex of the flow is (s), arriving at a sink vertex (t), and each graph edge permits a flow, constrained by a capacity.
The Ford-Fulkerson method and the Edmonds-Karp algorithm are remarkably similar, with the exception that the Edmonds-Karp algorithm finds augmented pathways to improve flow by using Breadth First Search (BFS).
==== EXAMPLE MUKAVU ====
In order to discover a road with available capacity from the source to the sink (referred to as an augmented path), the Edmonds-Karp algorithm employs Breadth-First Search (BFS). Next, it transmits as much flow as possible through that channel.
The Edmonds-Karp algorithm keeps looking for new ways to let more flow through until it reaches the maximum flow.
The maximum flow problem in the simulation above is resolved by the Edmonds-Karp algorithm: It determines the maximum flow that the source vertex can send.s to the vertex of the sink t, and eight is the maximum flow.
The numbers in the simulation above are written in fractions, where the first number is the flow, and the second number is the capacity (maximum possible flow in that edge). So for example, 0/7 on edge s→v2, means there is 0 flow, with a capacity of 7 on that edge.
The Edmonds-Karp algorithm’s fundamental step-by-step operation is shown here, but in order to truly comprehend it, we’ll need to delve into further depth later.
How it works:
1. Begin with no flow at any edge.
2. To locate an enhanced path where more flow can be conveyed, use BFS.
3. Determine the amount of flow that can be sent along that increased path by doing a bottleneck calculation.
4. In the enhanced path, increase the flow determined by the bottleneck calculation for every edge.
5. Until the maximum flow is reached, repeat steps 2-4. When a fresh augmented path is no longer possible to find, this occurs.
Residual Network in Edmonds-Karp
A residual network, or representation of the original graph, is created and utilized by the Edmonds-Karp method.
Each edge in the residual network has a residual capacity, which is equal to the edge’s initial capacity less the edge’s flow. The remaining capacity in an edge with some flow is known as the residual capacity.
For example, if there is a flow of 2 in the v3→v4 edge, and the capacity is 3, the residual flow is 1 in that edge, because there is room for sending 1 more unit of flow through that edge.
Reversed Edges in Edmonds-Karp
Reversed edges are another method that the Edmonds-Karp algorithm employs to return flow. This helps to improve the overall flow.
For every original edge in the network, a reverse edge is constructed in order to send flow back in the opposite direction of the edge. These reverse edges can then be used by the Edmonds-Karp algorithm to transfer flow in the opposite direction.
A reversed edge has residual capacity but neither flow nor capacity. A reversed edge’s residual capacity is always equal to the flow in the corresponding original edge.
In our example, the edge v1→v3has a flow of 2, which means there is a residual capacity of 2 on the corresponding reversed edge v3→v1.
This just means that when there is a flow of 2 on the original edge v1→v3, there is a possibility of sending that same amount of flow back on that edge, but in the reversed direction. Using a reversed edge to push back flow can also be seen as undoing a part of the flow that is already created.
The Edmonds-Karp algorithm relies heavily on the concepts of reversed edges and a residual network with residual capacity on edges; we will discuss these concepts in more detail when we use the algorithm later in this article.
Manual Run Through
The graph does not initially have any flow.
The first step of the Edmonds-Karp algorithm is to locate an augmented path where flow can be boosted by employing Breadth-First Search. s→v1.→v3.→t..
Following the identification of the enhanced path, the amount of flow that may be transmitted via it is determined by performing a bottleneck calculation. This flow is 2.
Thus, in the enhanced path, a flow of two is sent over each edge.
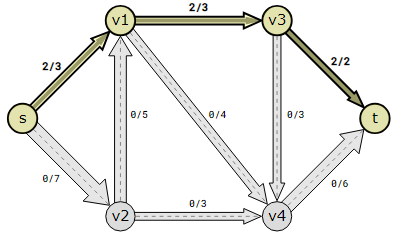
The following steps must be repeated in the Edmonds-Karp algorithm iteration: Determine the amount that the flow in a newly created augmented path can be raised, then increase the flow along the path’s edges in accordance with that determination.
The next augmented path is found to be s→v1→v4→t.
The flow can only be increased by 1 in this path because there is only room for one more unit of flow in the s→v1edge.
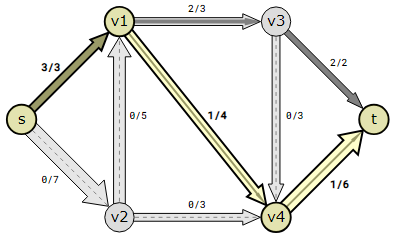
The next augmented path is found to be s→v2→v4→t.
The flow can be increased by 3 in this path. The bottleneck (limiting edge) is v2→v4because the capacity is 3.
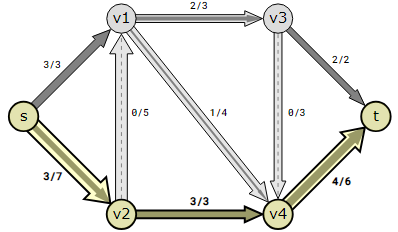
The last augmented path found is s→v2→v1→v4→t.
The flow can only be increased by 2 in this path because of edge v4→t being the bottleneck in this path with only space for 2 more units of flow (capacity−flow=1).
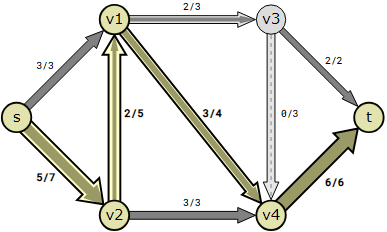
There isn’t currently a way to identify a new augmenting path, meaning that more flow cannot be transmitted via from s to t), indicating that the Edmonds-Karp procedure is complete when the maximum flow has been identified.
There is an eight-flow maximum. The figure above illustrates how the flow (8) exits the source is the same. vertex sas the stream entering the sink vertex t..
Also, if you take any other vertex than s or t, you can see that the amount of flow going into a vertex, is the same as the flow going out of it. This is what we call conservation of flow, and this must hold for all such flow networks (directed graphs where each edge has a flow and a capacity).
Implementation of The Edmonds-Karp Algorithm
The Edmonds-Karp algorithm is implemented by creating a Graph class.
The graph’s edges and vertices are represented by the graph:
class Graph:
def __init__(self, size):
self.adj_matrix = [[0] * size for _ in range(size)]
self.size = size
self.vertex_data = [''] * size
def add_edge(self, u, v, c):
self.adj_matrix[u][v] = c
def add_vertex_data(self, vertex, data):
if 0 <= vertex < self.size:
self.vertex_data[vertex] = data
Line 3: To store all of the edges and edge capacities, we build the adj_matrix. The starting point is set to 0.
Line 4: The graph’s size is determined by its vertex count.
Line 5: All of the vertices’ names are stored in the vertex_data.
Line 7-8: To add an edge with capacity c from vertex u to vertex v, use the add_edge method.
Lines 10–12: To add a vertex name to the graph, use the add_vertex_data method. The vertex name is data, and the vertex index is provided by the vertex parameter.
The bfs method, which finds enhanced pathways using Breadth-First-Search, is likewise included in the Graph class:
def bfs(self, s, t, parent):
visited = [False] * self.size
queue = [] # Using list as a queue
queue.append(s)
visited[s] = True
while queue:
u = queue.pop(0) # Pop from the start of the list
for ind, val in enumerate(self.adj_matrix[u]):
if not visited[ind] and val > 0:
queue.append(ind)
visited[ind] = True
parent[ind] = u
return visited[t]
Lines 15–18: When looking for an augmented path, the visited array helps to prevent returning to the same vertices. Vertices that need to be investigated are stored in a queue, and the search always begins at the source vertex.
Lines 20–21: Remove the initial vertex from the queue so that a path can be found from it to the next vertex, as long as there are vertices to be investigated in the queue.
Line 23: For each vertex that the current vertex is near to.
Lines 24-27: Add the neighboring vertex to the list of vertices that need to be investigated, mark it as visited, and set the parent of the adjacent vertex to be the current vertex u if it hasn’t been visited yet and there’s still capacity on its edge.
A path from the sink vertex to the source vertex is created backwards by storing the parent of a vertex in the parent array. The parent is employed to improve flow in the augmented path further on in the Edmonds-Karp algorithm—beyond the bfs approach.
Line 29: If the enhanced path stops at the sink node t, then the final line returns visited[t]. Finding an augmenting path indicates that the response is true.
The final method we add to the Graph class is called edmonds_karp:
def edmonds_karp(self, source, sink):
parent = [-1] * self.size
max_flow = 0
while self.bfs(source, sink, parent):
path_flow = float("Inf")
s = sink
while(s != source):
path_flow = min(path_flow, self.adj_matrix[parent[s]][s])
s = parent[s]
max_flow += path_flow
v = sink
while(v != source):
u = parent[v]
self.adj_matrix[u][v] -= path_flow
self.adj_matrix[v][u] += path_flow
v = parent[v]
path = []
v = sink
while(v != source):
path.append(v)
v = parent[v]
path.append(source)
path.reverse()
path_names = [self.vertex_data[node] for node in path]
print("Path:", " -> ".join(path_names), ", Flow:", path_flow)
return max_flow
The while loop increases the max_flow as long as there is an augmented path to increase flow in, therefore at first the parent array contains erroneous index values because there isn’t an enhanced path to begin with and the max_flow is 0.
Line 35: As long as there are augmented pathways for the Edmonds-Karp algorithm to increase flow along, the outer while loop ensures that the method continues to increase flow.
Lines 36–37: The sink vertex will be used to compute any potential increase in flow. The initial flow along an augmented path is limitless.
Line 38–40: By moving backward from the sink vertex in the direction of the source vertex, the value for path_flow can be determined. The maximum flow that can be sent down the path is determined by the lowest value of residual capacity along the way.
Line 42: Path_flow is increased by the path_flow
Lines 44–48: As you step through the augmented path and move backwards from the sink to the source, the path_flow on the forward edges reduces the residual capacity, and on the reversed edges, it increases it.
Lines 50–58: The purpose of this portion of the code is only to report the amount of flow that is routed through each augmented path that is discovered.
The vertices and edges of the particular graph must be defined after the Graph class has been defined in order to initialize it. The full code for the Edmonds-Karp algorithm example looks like this:
Example
Python:
class Graph:
def __init__(self, size):
self.adj_matrix = [[0] * size for _ in range(size)]
self.size = size
self.vertex_data = [''] * size
def add_edge(self, u, v, c):
self.adj_matrix[u][v] = c
def add_vertex_data(self, vertex, data):
if 0 <= vertex < self.size:
self.vertex_data[vertex] = data
def bfs(self, s, t, parent):
visited = [False] * self.size
queue = [] # Using list as a queue
queue.append(s)
visited[s] = True
while queue:
u = queue.pop(0) # Pop from the start of the list
for ind, val in enumerate(self.adj_matrix[u]):
if not visited[ind] and val > 0:
queue.append(ind)
visited[ind] = True
parent[ind] = u
return visited[t]
def edmonds_karp(self, source, sink):
parent = [-1] * self.size
max_flow = 0
while self.bfs(source, sink, parent):
path_flow = float("Inf")
s = sink
while(s != source):
path_flow = min(path_flow, self.adj_matrix[parent[s]][s])
s = parent[s]
max_flow += path_flow
v = sink
while(v != source):
u = parent[v]
self.adj_matrix[u][v] -= path_flow
self.adj_matrix[v][u] += path_flow
v = parent[v]
path = []
v = sink
while(v != source):
path.append(v)
v = parent[v]
path.append(source)
path.reverse()
path_names = [self.vertex_data[node] for node in path]
print("Path:", " -> ".join(path_names), ", Flow:", path_flow)
return max_flow
# Example usage:
g = Graph(6)
vertex_names = ['s', 'v1', 'v2', 'v3', 'v4', 't']
for i, name in enumerate(vertex_names):
g.add_vertex_data(i, name)
g.add_edge(0, 1, 3) # s -> v1, cap: 3
g.add_edge(0, 2, 7) # s -> v2, cap: 7
g.add_edge(1, 3, 3) # v1 -> v3, cap: 3
g.add_edge(1, 4, 4) # v1 -> v4, cap: 4
g.add_edge(2, 1, 5) # v2 -> v1, cap: 5
g.add_edge(2, 4, 3) # v2 -> v4, cap: 3
g.add_edge(3, 4, 3) # v3 -> v4, cap: 3
g.add_edge(3, 5, 2) # v3 -> t, cap: 2
g.add_edge(4, 5, 6) # v4 -> t, cap: 6
source = 0; sink = 5
print("The maximum possible flow is %d " % g.edmonds_karp(source, sink))
Time Complexity for The Edmonds-Karp Algorithm
Edmonds-Karp and Ford-Fulkerson are different in that Edmonds-Karp finds augmented pathways using Breadth-First Search (BFS) and Ford-Fulkerson uses Depth-First Search (DFS).
This indicates that since Edmonds-Karp is unaffected by the maximum flow value, it is easier to anticipate how long it will take to run than Ford-Fulkerson.
Given the quantity of vertices Vthe quantity of edges Ethe Edmonds-Karp algorithm’s time complexity is
O(V⋅E2)
This indicates that, unlike Ford-Fulkerson, Edmonds-Karp depends on the number of vertices and edges rather than the maximum flow.
The reason we get this time complexity for Edmonds-Karp is that it runs BFS which has time complexity O(E+V).
But if we assume a bad case scenario for Edmonds-Karp, with a dense graph, where the number of edges E is much greater than the number of vertices V, time complexity for BFS becomes O(E).
BFS must run one time for every augmented path, and there can actually be found close to V⋅E augmented paths during running of the Edmonds-Karp algorithm.
So, BFS with time complexity O(E) can run close to V⋅E times in the worst case, which means we get a total time complexity for Edmonds-Karp: O(V⋅E⋅E)=O(V⋅E2).
