DSA Simple Algorithm
Fibonacci Numbers
Here is a quick introduction to the Fibonacci numbers before we go on because they are a great tool for introducing algorithms.
Fibonacci, an Italian mathematician from the 13th century, is the name of the Fibonacci numbers.
Fibonacci numbers have two initial values, 0 and 1. The subsequent Fibonacci number is determined by adding the two preceding values; thus, we obtain 0, 1, 1, 2, 3, 5, 8, 13, 21,…
----- IMAGE MUKAVI ----
There will be a lot of looping and recursion in this lesson. To quickly demonstrate the differences between programming with loops and programming with recursion, let’s develop three distinct versions of the algorithm to create Fibonacci numbers before moving on.
The Fibonacci Number Algorithm
All we have to do is add the two previous Fibonacci numbers to get a new one.
An effective technique to illustrate what an algorithm is is to use the Fibonacci numbers. Since we understand the basic idea behind finding the next number, we can develop an algorithm that generates as many Fibonacci numbers as feasible.
The formula for producing the first 20 Fibonacci numbers is shown below.
How it works:
1.Start with the two first Fibonacci numbers 0 and 1.
a.Add the two previous numbers together to create a new Fibonacci number.
b.Update the value of the two previous numbers.
2.Do point a and b above 18 times.
Loops vs Recursion
We will use three distinct approaches to create methods to discover Fibonacci numbers in order to demonstrate the distinction between loops and recursion:
1. An implementation of the Fibonacci algorithm above using a for loop.
2. An implementation of the Fibonacci algorithm above using recursion.
3. Finding the nth Fibonacci number using recursion.
1. Implementation Using a For Loop
Before writing the code, it can be a good idea to make a list of what it needs to do or contain:
- Two variables to hold the previous two Fibonacci numbers
- A for loop that runs 18 times
- Create new Fibonacci numbers by adding the two previous ones
- Print the new Fibonacci number
- Update the variables that hold the previous two fibonacci numbers
It is simpler to write the program if you use the above list:
Example
prev2 = 0
prev1 = 1
print(prev2)
print(prev1)
for fibo in range(18):
newFibo = prev1 + prev2
print(newFibo)
prev2 = prev1
prev1 = newFibo
2. Implementation Using Recursion
A function that calls itself is called recursive.
The majority of the components needed to implement the Fibonacci algorithm are the same as those in the code sample above; however, recursion must be used in place of the for loop.
Much of the code must be contained in a function in order to replace the for loop with recursion. The function must also call itself to generate a new Fibonacci number if the total number of Fibonacci numbers it produces is less than or equal to 19.
This is how our code appears:
Example
print(0)
print(1)
count = 2
def fibonacci(prev1, prev2):
global count
if count <= 19:
newFibo = prev1 + prev2
print(newFibo)
prev2 = prev1
prev1 = newFibo
count += 1
fibonacci(prev1, prev2)
else:
return
fibonacci(1,0)
3. Finding The nth Fibonacci Number Using Recursion
We can develop code based on the mathematical formula for the Fibonacci number to determine the nth Fibonacci number n:
F(n)=F(n−1)+F(n−2)
In other words, the 10th Fibonacci number, for instance, is the product of the 9th and 8th Fibonacci numbers.
Note: This formula uses a 0-based index. This means that to generate the 20th Fibonacci number, we must write
F(19).
As long as n is less than or equal to 1, we can use this idea with recursion and allow the function to call itself. If
n≤1. it indicates that either of the first two Fibonacci numbers—1 or 0—has been reached during code execution.
This is how the code appears:
Example
def F(n):
if n <= 1:
return n
else:
return F(n - 1) + F(n - 2)
print(F(19))
You’ll see that this recursive procedure makes two calls to itself instead of simply one. This has a significant impact on how the software functions on our machine. As we increase the desired Fibonacci number, the number of calculations will skyrocket. To be more exact, each time we increase the desired Fibonacci number by one, the number of function calls will double.
Simply observe how many function calls there are for F(5):
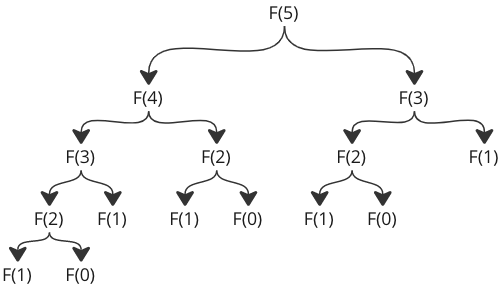
To better understand the code, here is how the recursive function calls return values so that
F(5) returns the correct value in the end:
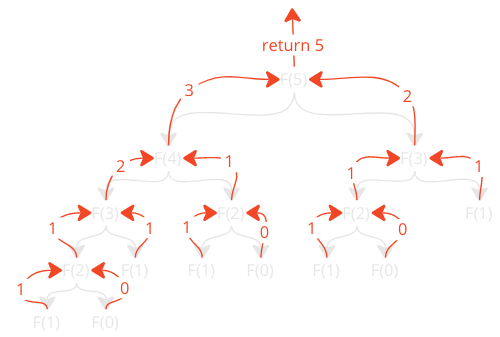
The number of function calls and the number of times the function is called with the same arguments are the two crucial items to pay attention to in this case.
Therefore, even though the code is interesting and demonstrates how recursion works, it is not useful for producing huge Fibonacci numbers because of how slowly and ineffectively it executes.
Summary
Let’s take a look at what we have so far before moving on:
- An algorithm can be implemented in different ways and in different programming languages.
- Recursion and loops are two different programming techniques that can be used to implement algorithms.
It’s time to examine the array, which is the first data structure we will examine.
