DSA Selection Sort
Selection Sort
The array’s lowest value is located and moved to the front by the Selection Sort algorithm.
------ IMAGE MUKAVI -----
Until the array is sorted, the algorithm repeatedly scans over it, pushing the next lowest values to the front.
How it works:
1.Go through the array to find the lowest value.
2.Move the lowest value to the front of the unsorted part of the array.
3.Go through the array again as many times as there are values in the array.
To gain a thorough understanding of the Selection Sort algorithm and how to use it yourself, keep reading.
Manual Run Through
To obtain a sense of the Selection Sort method, let’s manually loop over a small array just once before implementing it in a computer language.
Step 1: With an unsorted array at first.
[7, 12, 9, 11, 3]
Step 2: Examine each value in the array one at a time. What is the lowest value? 3, am I correct?
[ 7, 12, 9, 11, 3]
Step 3: Place value 3, which is the lowest, at the front of the array.
[ 3, 7, 12, 9, 11]
Step 4: Examine the remaining values, beginning with 7. We don’t need to shift value 7, as it is the lowest value and is already at the head of the array.
[ 3, 7, 12, 9, 11]
Step 5: Examine the last three arrays: 12, 9, and 11. The lowest number is 9.
[ 3, 7, 12, 9, 11]
Step 6: 9 should advance to the front.
[ 3, 7, 9, 12, 11]
Step 7: Of the two, 11 is the lowest when comparing.
[ 3, 7, 9, 12, 11]
Step 8: Shift it forward.
[ 3, 7, 9, 11, 12]
The array is sorted at the end.
The following steps can be seen animated by running the simulation:
------ IMAGE MUKAVI -----
Manual Run Through: What Happened?
To completely comprehend the method and be able to implement it in a programming language, we need to grasp what transpired above.
What became of the lowest value, 3, can you see? It has been moved to the beginning of the array in step 3, where it belongs, but the array is still unsorted at that point.
As a result, the Selection Sort algorithm needs to repeatedly iterate through the array, moving the next lowest value to its proper location in front of the unsorted portion of the array each time. Sorting keeps going until the array’s final value, 12, is the highest value still present. This indicates that in order to sort the array of five items, we must iterate through the array four times.
Additionally, the length of the array’s remaining unsorted portion decreases with each iteration of the process.
The Selection Sort algorithm will now be implemented in a programming language using the knowledge we have gained.
Selection Sort Implementation
The Selection Sort algorithm requires the following to be implemented in a programming language:
1.An array with values to sort.
2.An inner loop that goes through the array, finds the lowest value, and moves it to the front of the array. This loop must loop through one less value each time it runs.
3.An outer loop that controls how many times the inner loop must run. For an array with n values, this outer loop must run n − 1 times.
The code that is produced looks like this:
Example
my_array = [64, 34, 25, 5, 22, 11, 90, 12]
n = len(my_array)
for i in range(n-1):
min_index = i
for j in range(i+1, n):
if my_array[j] < my_array[min_index]:
min_index = j
min_value = my_array.pop(min_index)
my_array.insert(i, min_value)
print("Sorted array:", my_array)
Selection Sort Shifting Problem
There is still need for slight improvement in the Selection Sort algorithm.
The code above inserts the element with the lowest value in front of the array after removing it.
To compensate for the removal of the next lowest value array element, all subsequent items must be pushed one place down.

We’re still not quite done with this shifting process, which takes a long time! The lowest value,(5), is located and eliminated before being inserted at the beginning of the array. As the graphic below illustrates, any values that come after it must move up one position to make room for the new value.
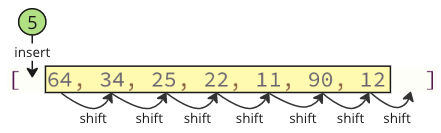
Note: If you are using a high level programming language like Python or Java, you won’t see these shifting operations occurring in the code; nonetheless, they are still occurring in the background. The computer has to spend more time performing such shifting tasks, which can be problematic.
Solution: Swap Values!
Instead of all the shifting, swap the lowest value (5) with the first value (64) like below.

Because the lowest value always ends up in the right place and is not yet sorted, it does not matter where we put the other value we are swapping with. This allows us to swap values as the image above illustrates.
This simulation demonstrates the operation of the enhanced Selection Sort with swapping:
------ IMAGE MUKAVI -----
This is an example of how to use swapping to achieve the enhanced Selection Sort:
Example
my_array = [64, 34, 25, 12, 22, 11, 90, 5]
n = len(my_array)
for i in range(n):
min_index = i
for j in range(i+1, n):
if my_array[j] < my_array[min_index]:
min_index = j
my_array[i], my_array[min_index] = my_array[min_index], my_array[i]
print("Sorted array:", my_array)
Selection Sort Time Complexity
See this article for a broad description of time complexity.
See this page for a more comprehensive and in-depth explanation of Selection Sort time complexity.
Selection Sort arranges a range of n principles.
In general, around n/2. To determine the lowest value in each loop, elements are compared.
In order to locate the lowest value, Selection Sort must execute the loop around n times.
Time complexity is obtained:
O(n2⋅n)=O(n2)
A graph similar to this one can be used to show the Selection Sort algorithm’s time complexity:

As you can see, the run time is the same as for Bubble Sort: as the array size increases, the run time grows exponentially.
Try the following simulation with varying array sizes.
The red dashed line represents the theoretical time complexity O(n)2 squre.
Start the simulation, and you should see blue crosses. The number of operations required to sort an array of a specific size is indicated by the blue crosses.
------ IMAGE MUKAVI -----
The most significant difference from Bubble sort that we can notice in this simulation is that best and worst case is actually almost the same for Selection Sort (O(n2)), but for Bubble Sort the best case runtime is only O(n).
The number of swaps is the primary factor separating the best case from the worst scenario for Selection Sort. The array is already sorted, thus in the best situation, Selection Sort doesn’t need to swap any values. In the worst situation, Selection Sort will need to do as many swaps as there are values in the array because the array has already been sorted, albeit in the incorrect order.
