DSA Quick Sort
DSA Quicksort
Quicksort is among the quickest sorting algorithms, as its name implies.
After selecting one value from the array to serve as the “pivot” element, the Quicksort algorithm rearranges the other values so that the pivot element is on the left and the higher values are on the right.
------ IMAGE MUKAVI -----
The pivot element in this example is the last element in the array, but we could have chosen any element in the array, or even the first element.
Next, on the sub-arrays on the left and right of the pivot element, the Quicksort algorithm does the same action recursively. Until the array is sorted, this is done.
A function that calls itself is called recursive.
Following the pivot element’s placement between a sub-array on the left with lower values and a sub-array on the right with higher values, the Quicksort algorithm calls itself twice, repeating the Quicksort process for the left and right sub-arrays. In order to sort the sub-arrays, the Quicksort algorithm keeps calling itself until they are too small.
This is how the algorithm can be explained:
How it works:
1.Select a value from the array to serve as the pivot point.
2.Arrange the remaining values in the array so that they are higher on the right and lower than the pivot element on the left.
3.To have the pivot element lie between the lower and higher values, swap it with the first element of the higher values.
4.For the sub-arrays on the left and right sides of the pivot element, perform the identical actions (recursively).
To gain a thorough understanding of the Quicksort algorithm and how to use it yourself, keep reading.
Manual Run Through
To gain an understanding of the Quicksort method, let’s manually traverse a brief array prior to implementing it in a computer language.
Step 1: An unsorted array is where we begin.
[ 11, 9, 12, 7, 3]
Step 2: The final value, 3, is selected as the pivotal point.
[ 11, 9, 12, 7, 3]
Step 3: All of the remaining values in the array must be on the right side of three and greater than three. Replace 3 with 11.
[ 3, 9, 12, 7, 11]
Step 4: Value 3 is now positioned correctly. The values must be sorted to the right of 3. The final value, 11, is our new pivot point.
[ 3, 9, 12, 7, 11]
Step 5: The pivot values, 11 and 12, must be located to the left and right of each other, respectively. Steps 7 and 12.
[ 3, 9, 7, 12, 11]
Step 6: Exchange 11 and 12 so that 11 is on the right side and the lower numbers, 9 and 7, are on the left.
[ 3, 9, 7, 11, 12]
Step 7: Eleven and twelve are positioned correctly. To the left of 11, we designate 7 as the pivot element in the sub-array [9, 7].
[ 3, 9, 7, 11, 12]
Step 8: We have to exchange 9 for 7.
[ 3, 7, 9, 11, 12]
The array has now been sorted.
The following steps can be seen animated by running the simulation:
------ IMAGE MUKAVI -----
Manual Run Through: What Happened?
We must go over the events from above in further depth before we can put the method into practice in a programming language.
As we’ve already seen, the array’s final value is selected as its pivot element, and the remaining values are organized with the pivot value on the left and the higher values on the right.
Subsequently, the pivot element is replaced with the initial greater value. With the pivot element positioned between the lower and higher values, this divides the original array in half.
With the sub-arrays on the left and right sides of the previous pivot element, we must now proceed as before. Additionally, a sub-array is deemed completely sorted if its length is either 0 or 1.
In summary, until the array is sorted, the Quicksort algorithm causes the sub-arrays to get shorter and shorter.
Quicksort Implementation
Recursion is used to create a ‘quickSort’ function that divides the array into progressively shorter sub-arrays. Consequently, the new sub-arrays to the left and right of the pivot element must be passed to the ‘quickSort’ method when it calls itself. Go here to learn more about recursion.
In a computer language, the Quicksort algorithm has to be implemented using:
1.An array to be sorted by values.
2.A quickSort function that, in the event that the sub-array’s size is more than 1, calls itself (recursion).
3.a partitioning technique that takes in a sub-array, reorders values, switches the pivot element within the sub-array, and returns the index of the subsequent sub-array split.
The code that is produced looks like this:
Example
def partition(array, low, high):
pivot = array[high]
i = low - 1
for j in range(low, high):
if array[j] <= pivot:
i += 1
array[i], array[j] = array[j], array[i]
array[i+1], array[high] = array[high], array[i+1]
return i+1
def quicksort(array, low=0, high=None):
if high is None:
high = len(array) - 1
if low < high:
pivot_index = partition(array, low, high)
quicksort(array, low, pivot_index-1)
quicksort(array, pivot_index+1, high)
my_array = [64, 34, 25, 12, 22, 11, 90, 5]
quicksort(my_array)
print("Sorted array:", my_array)
Quicksort Time Complexity
See this article for a broad description of time complexity.
See this page for a more comprehensive and in-depth description of Quicksort time complexity.
In the worst situation, Quicksort’s O(n)2 squre.. This results in a large number of recursive calls since the pivot element is either the highest or lowest value in each sub-array. This occurs when the array is already sorted in the example implementation we used earlier.
But on average, the time complexity for Quicksort is actually just O(nlogn), which is a lot better than for the previous sorting algorithms we have looked at. That is why Quicksort is so popular.
Below you can see the significant improvement in time complexity for Quicksort in an average scenario O(nlogn), compared to the previous sorting algorithms Bubble, Selection and Insertion Sort with time complexity O(n2):
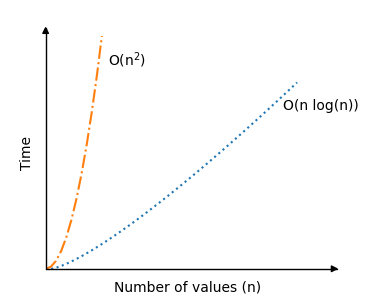
Because the array will be split in half fairly evenly each time the Quicksort algorithm calls itself, the recursion portion of the algorithm is actually the reason why the average sorting situation is so quick. Therefore, even if the number of values n doubles, the number of recursive calls does not.
Use Quicksort on various array types with varying numbers of values as demonstrated in the simulation below:
