DSA Counting Sort
Counting Sort
By counting the occurrences of each value in an array, the Counting Sort algorithm organizes the data.
------image mukiavi ------
Try the simulation to observe how counting sort is used to sort 17 integer numbers from 1 to 5.
Unlike the prior sorting algorithms we have seen, counting sort only operates on non-negative integers and does not compare values.
Moreover, counting sorting happens quickly when there are fewer values \(n\) than there are alternative values \(k\).
How it works:
1.To count how many of the various values there are, create a new array.
2.Examine each element in the array that has to be sorted.
3.Increase the counting array at the appropriate index to count each value.
4.Create the sorted array by iterating through the counting array once the items have been counted.
5.Make the appropriate number of items for each count in the counting array, with values that match the index of the counting array.
Conditions for Counting Sort
It is believed that Counting Sort is only effective for a restricted range of non-negative integer values for the following reasons:
- Integer values: Since counting occurrences of distinct values is the foundation of counting sort, the values must be integers. With integers, there is a finite number of possible values \(k\) that are not excessively greater than the number of values \(n\). Each value fits with an index (for non-negative values).
- Non negative values: Counting Usually, sort is accomplished by building a counting array. Value x is counted by raising the value of the counting array at index x as the algorithm runs through the values that need to be sorted. Sorting value -3 would be problematic if we were to sort negative values as index -3 is outside of the counting array.
- Limited range of values: The counting array we need for sorting will be larger than the original array we have that needs sorting, and the process will become ineffective if the number of possible alternative values to be sorted \(k\) is more than the number of values to be sorted \(n\).
Manual Run Through
To gain an understanding of the Counting Sort method, let’s manually traverse a brief array prior to implementing it in a computer language.
Step 1: An unsorted array is where we begin.
myArray = [ 2, 3, 0, 2, 3, 2]
Step 2: To count the number of each value, we build another array. With four elements, the array may store values 0 through 3.
myArray = [ 2, 3, 0, 2, 3, 2]
countArray = [ 0, 0, 0, 0]
Step 3: Let’s begin counting now. Since there is a 2 in the first entry, the counting array element at index 2 needs to be increased.
myArray = [ 2, 3, 0, 2, 3, 2]
countArray = [ 0, 0, 1, 0]
Step 4: After a value has been counted, it can be eliminated and the subsequent value, 3, can be counted.
myArray = [ 3, 0, 2, 3, 2]
countArray = [ 0, 0, 1, 1]
Step 5: Since index 0 in the counting array is the next number to be counted, we increase it.
myArray = [ 0, 2, 3, 2]
countArray = [ 1, 0, 1, 1]
Step 6: We keep going in this manner until every value has been tallied.
myArray = [ ]
countArray = [ 1, 0, 3, 2]
Step 7: The elements from the original array will now be recreated, and this time, they will be arranged from lowest to highest.
We have one element with a value of 0 according to the first entry in the counting array. Thus, we decrease the element at index 0 in the counting array by 1 and push 1 element with value 0 into the array.
myArray = [ 0]
countArray = [ 0, 0, 3, 2]
Step 8: The counting array indicates that there is no need for us to construct any elements with a value of 1.
myArray = [ 0]
countArray = [ 0, 0, 3, 2]
Step 9: We advance three elements with a value of two to the array’s end. Additionally, we reduce the counting array at index 2 as we add these elements.
myArray = [ 0, 2, 2, 2]
countArray = [ 0, 0, 0, 2]
Step 10: To complete the array, we need to add two items with a value of 3.
myArray = [0, 2, 2, 2, 3, 3]
countArray = [ 0, 0, 0, 0]
At last! Sorting is done on the array.
The following steps can be seen animated by running the simulation:
------ IMAGE MUKAVI -----
Manual Run Through: What Happened?
We must go over the events from above in further depth before we can put the method into practice in a programming language.
The Counting Sort algorithm operates in two stages, as we’ve seen:
1.By incrementing at the appropriate index in the counting array, each value is counted. A value is eliminated once it has been counted.
2.Using the count and count index from the counting array, the values are replicated in the correct sequence.
Keeping this in mind, we can begin putting the algorithm into practice with Python.
Counting Sort Implementation
In a programming language, the Counting Sort algorithm has to be implemented using:
1.An array to be sorted by values.
2.a ‘countingSort’ function that takes an integer array as input.
3.An array contained within the procedure to maintain the value count.
4.a loop within the procedure that increases the number of entries in the counting array in order to count and eliminate values.
5.a loop within the procedure that uses the counting array to regenerate the array and ensure that the elements appear in the correct order.
One more thing: To generate the counting array with the proper size, we must determine the highest value in the array. To count all conceivable non-negative integers, such as 0, 1, 2, 3, 4, and 5, the counting array must have a total of 6 entries, for instance, if the highest number is 5.
The code that is produced looks like this:
Example
def countingSort(arr):
max_val = max(arr)
count = [0] * (max_val + 1)
while len(arr) > 0:
num = arr.pop(0)
count[num] += 1
for i in range(len(count)):
while count[i] > 0:
arr.append(i)
count[i] -= 1
return arr
unsortedArr = [4, 2, 2, 6, 3, 3, 1, 6, 5, 2, 3]
sortedArr = countingSort(unsortedArr)
print("Sorted array:", sortedArr)
Counting Sort Time Complexity
See this article for a broad description of time complexity.
See this page for a more comprehensive and in-depth discussion of Insertion Sort time complexity.
The range of available values and the counting sort algorithm’s processing speed are related.
In general, time complexity for Counting Sort is O(n+k).
In a best case scenario, the range of possible different values k is very small compared to the number of values n and Counting Sort has time complexity O(n).
But in a worst case scenario, the range of possible different values k is very big compared to the number of values n and Counting Sort can have time complexity O(n2) or even worse.
The following graphic illustrates the range of possible time complexity for Counting Sort.
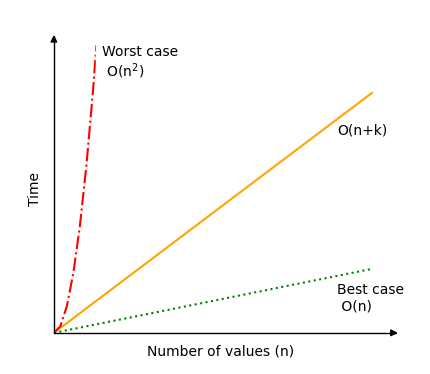
As you can see, before selecting Counting Sort as your algorithm, it is crucial to take into account the range of values in relation to the number of items to be sorted. Additionally, bear in mind that Counting Sort is limited to non-negative integer values, as stated at the top of the page.
Run different simulations of Counting Sort to see how the number of operations falls between the worst case scenario O(n2) (red line) and best case scenario O(n) (green line).
------ IMAGE MUKAVI -----
As mentioned previously: if the numbers to be sorted varies a lot in value (large k), and there are few numbers to sort (small n), the Counting Sort algorithm is not effective.If n is held, and k Thus, the number of operations is the same for the “Random,” “Descending,” and “Ascending” possibilities in the scenario above. This is due to the fact that all three scenarios have the same outcome: After setting up a counting array and counting the integers, a new sorted array is produced.
