DSA Bubble Sort
Bubble Sort
An array is sorted using the bubble sort algorithm from lowest value to highest value.
------ IMAGE MUKAVI -----
To show what happens when the Bubble Sort algorithm sorts an array of values, run the simulation. A column in the array represents each value.
The way this algorithm operates—making the highest numbers “bubble up”—is where the word “bubble” originates.
How it works:
1.Go through the array, one value at a time.
2.For each value, compare the value with the next value.
3.If the value is higher than the next one, swap the values so that the highest value comes last.
4.Go through the array as many times as there are values in the array.
To get a thorough understanding of the Bubble Sort algorithm and learn how to use it yourself, keep reading.
Manual Run Through
To gain a sense of the Bubble Sort method, let’s manually loop over a small array just once before implementing it in a programming language.
Step 1: With an unsorted array at first.
[7, 12, 9, 11, 3]
Step 2: We examine the first two values. Which value comes first, the lowest one? Indeed, thus there’s no need to switch them.
[7, 12, 9, 11, 3]
Step 3: Proceed a step farther and examine the numbers 12 and 9. Which value comes first, the lowest one? No.
[7, 12, 9, 11, 3]
Step 4: To make 9 come first, we must thus switch them.
[7, 9, 12, 11, 3]
Step 5: Moving forward a step, observing 12 and 11.
[7, 9, 12, 11, 3]
Step 6: So that 11 comes before 12, we have to switch.
[7, 9, 11, 12, 3]
Step 7: Considering numbers 12 and 3, should we switch them? Indeed.
[7, 9, 11, 12, 3]
Step 8: reversing 12 and 3 to have 3 appear first.
[7, 9, 11, 3, 12]
To watch the animation of the eight stages above, run the simulation below:
------ IMAGE MUKAVI -----
Manual Run Through: What Happened?
To properly grasp the algorithm and be able to implement it in a programming language, we need to understand what went wrong in this initial run through of the method.
What became of the highest value, 12, can you see? It has risen to the end of the array, its proper location. However, the array is still unsorted in its entirety.
Because of this, the Bubble Sort algorithm needs to iterate through the array multiple times, each time moving the next highest value closer to the right place. Until the lowest number, 3, remains at the beginning of the array, the sorting process is repeated. This indicates that in order to sort the array of five items, we must iterate through the array four times.
Additionally, the length of the array’s remaining unsorted portion decreases with each iteration of the process.
This is the appearance of a complete manual go through:
------ IMAGE MUKAVI -----
The Bubble Sort method will now be implemented in a programming language using the knowledge we have gained.
Bubble Sort Implementation
In order to put the Bubble Sort algorithm into practice in a programming language, we require:
1.An array to be sorted by values.
2.an internal loop that iterates across the array, switching values if the value at the beginning is greater than the value at the end. Every time it runs, this loop has to loop through one fewer value.
3.An outer loop that sets the maximum number of times the inner loop can run. An array containing n values requires this outer loop to execute n-1 times.
The code that is produced looks like this:
Example
my_array = [64, 34, 25, 12, 22, 11, 90, 5]
n = len(my_array)
for i in range(n-1):
for j in range(n-i-1):
if my_array[j] > my_array[j+1]:
my_array[j], my_array[j+1] = my_array[j+1], my_array[j]
print("Sorted array:", my_array)
Bubble Sort Improvement
There is still room for slight improvement in the Bubble Sort algorithm.
Assume that the array has nearly finished sorting, with the lowest integers at the beginning, for instance:
my_array = [7, 3, 9, 12, 11]
Under this scenario, the array will be sorted following the initial run, but the Bubble Sort algorithm will carry on without exchanging elements—which is not required.
The array must be fully sorted if the algorithm iterates through it once without changing any values. In this case, we can end the algorithm as follows:
Example
my_array = [7, 3, 9, 12, 11]
n = len(my_array)
for i in range(n-1):
swapped = False
for j in range(n-i-1):
if my_array[j] > my_array[j+1]:
my_array[j], my_array[j+1] = my_array[j+1], my_array[j]
swapped = True
if not swapped:
break
print("Sorted array:", my_array)
Bubble Sort Time Complexity
See this article for a broad description of time complexity.
See this page for a more comprehensive and in-depth description of Bubble Sort time complexity.
Every value in the array is iterated through and compared to the value adjacent to it using the Bubble Sort algorithm. Consequently, for an array of n items, there n such a loop of comparisons.
Additionally, the array is looped through n times after the first loop.
Therefore, there are n ⋅ n overall comparisons made, so Bubble Sort’s time complexity is:
O(n)2
This is the graph that illustrates the Bubble Sort time complexity:
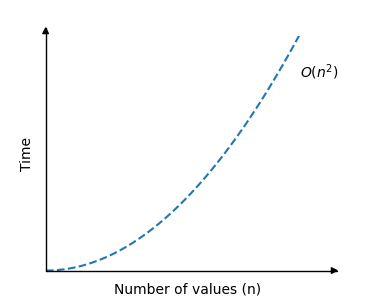
As you can see, as the array size increases, the run time grows very quickly.
Fortunately, quicker sorting algorithms exist, such as Quicksort, which we will examine later.
You can simulate Bubble Sort below, where the red and dashed line is the theoretical time complexity O(n)2 squre. You can choose a number of values n, and run an actual Bubble Sort implementation where the operations are counted and the count is marked as a blue cross in the plot below. How does theory compare with practice?
