DSA Insertion Sort
Insertion Sort
One portion of the array is used by the Insertion Sort algorithm to hold the sorted values, and the other portion is used to hold the unsorted values.
------ IMAGE MUKAVI -----
Until the array is sorted, the method takes one value at a time from the unsorted portion and inserts it into the appropriate location in the sorted portion of the array.
How it works:
1.Select the first value from the array’s unsorted section.
2.Place the value in the appropriate location within the array’s sorted section.
3.Repeat the process across the array’s unsorted section as many times as there are values.
To get a thorough understanding of the Insertion Sort algorithm and learn how to use it yourself, keep reading.
Manual Run Through
To gain an understanding of the Insertion Sort method, let’s manually traverse a brief array prior to implementing it in a computer language.
Step 1: With an unsorted array at first.
[7, 12, 9, 11, 3]
Step 2: The array’s first value can be thought of as its initial sorted portion. It needs to be sorted if there is just one value, right?
[ 7, 12, 9, 11, 3]
Step 3: In the array’s sorted portion, value 12 should now be moved to its proper location. However, since 12 is more than 7, it is already in the right place.
[ 7, 12, 9, 11, 3]
Step 4: Think about the following number, nine.
[ 7, 12, 9, 11, 3]
Step 5: Now that the value 9 needs to be shifted into the proper location inside the array’s sorted portion, we do so by shifting it between 7 and 12.
[ 7, 9, 12, 11, 3]
Step 6: Eleven is the next value.
[ 7, 9, 12, 11, 3]
Step 7: We shift it to the sorted portion of the array, between 9 and 12.
[ 7, 9, 11, 12, 3]
Step 8: Three is the final number to be inserted into the proper location.
[ 7, 9, 11, 12, 3]
Step 9: Since 3 is the lowest value, we place it in front of all other values
[ 3,7, 9, 11, 12]
The array is sorted at the end.
The following steps can be seen animated by running the simulation:
------ IMAGE MUKAVI -----
Manual Run Through: What Happened?
To completely comprehend the method and be able to implement it in a programming language, we need to grasp what transpired above.
The array’s first value is regarded as its initial sorted portion.
To ensure that each value is placed into the proper place, it must be compared to the values in the sorted portion of the algorithm after the initial value.
Since we do not need to sort the first item, the Insertion Sort Algorithm needs to iterate through the array four times in order to sort the array of five values.
Additionally, the length of the array’s remaining unsorted portion decreases with each iteration of the process.
The Insertion Sort method will now be implemented in a programming language using the knowledge we have gained.
Insertion Sort Implementation
1.An array with values to sort.
2.An outer loop that picks a value to be sorted. For an array with n values, this outer loop skips the first value, and must run n−1 times.
3.An inner loop that goes through the sorted part of the array, to find where to insert the value. If the value to be sorted is at index i, the sorted part of the array starts at index 0 and ends at index i−1.
The code that is produced looks like this:
Example
my_array = [64, 34, 25, 12, 22, 11, 90, 5]
n = len(my_array)
for i in range(1,n):
insert_index = i
current_value = my_array.pop(i)
for j in range(i-1, -1, -1):
if my_array[j] > current_value:
insert_index = j
my_array.insert(insert_index, current_value)
print("Sorted array:", my_array)
Insertion Sort Improvement
It makes sense how the code above first removes a value before inserting it somewhere else. It’s similar to how Insertion Sort is done physically, like with a deck of cards. You take up a fresh unsorted card and place it in the appropriate space between the other previously sorted cards if low value cards are sorted to the left.
The issue with this programming approach is that all elements above need to be relocated one index point down in order to remove a value from the array:
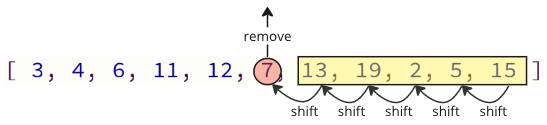
Additionally, there are numerous shift operations that need to be performed when adding the deleted value back into the array. To create room for the inserted value, the following items must all move up one position:
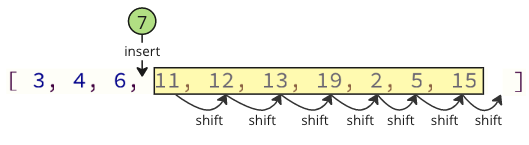
These shifting operations can be very time-consuming, particularly when dealing with large arrays.
Note: If you are using a high level programming language like Python or Java, you won’t see these shifting operations occurring in the code; nonetheless, they are still occurring in the background. The computer has to spend more time performing such shifting tasks, which can be problematic.
Improved Solution
By changing only the values that are required, we can skip the majority of these shift operations:
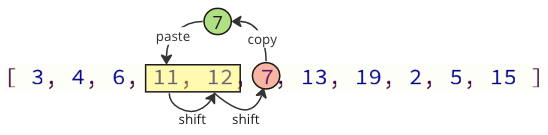
In the preceding image, value 7 is copied first, followed by values 11 and 12 being moved up one position in the array, and finally, value 7 is placed in the location where value 11 was previously.
In this instance, there are two shifting operations instead of twelve.
The example that follows demonstrates this improvement in action:
Example
my_array = [64, 34, 25, 12, 22, 11, 90, 5]
n = len(my_array)
for i in range(1,n):
insert_index = i
current_value = my_array[i]
for j in range(i-1, -1, -1):
if my_array[j] > current_value:
my_array[j+1] = my_array[j]
insert_index = j
else:
break
my_array[insert_index] = current_value
print("Sorted array:", my_array)
The aforementioned code also breaks out of the inner loop. This is due to the fact that once we have determined where the current value should be, there is no need to compare values further.
Insertion Sort Time Complexity
See this article for a broad description of time complexity.
See this page for a more comprehensive and in-depth discussion of Insertion Sort time complexity.
Selection Sort arranges a range of n principles.
On average, each value must be compared to about n/2 other values to find out where to insert it.
Additionally, Selection Sort needs to execute the loop n times or so in order to put a value in the proper location.
The Insertion Sort time complexity is as follows:
O(n2⋅n)=O(n2)
This is one way to show the Insertion Sort time complexity:

Check out the simulation below to observe how the theoretical O(n)2 squre (Red Line) contrasts with the actual number of Insertion Sort operations.
------ IMAGE MUKAVI -----
There is a significant distinction between the best, average, and worst case possibilities for Insertion Sort. You can test it by executing the various simulations mentioned above.
Quicksort is the next in line. It’s finally happening—a quicker sorting algorithm!
